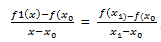MAKALAH
INTERPOLASI LINEAR,
KUADRAT, KUBIK & POLINOM LAGRANGE
OLEH:
• EMAN SULAEMAN (52411423)
• HAJIL ZULHI JAMALUDIN (53411156)
• PRAJUDI WILLIAM CHRISDEAR (55411549)
TEKNIK INFORMATIKA
UNIVERSITAS GUNADARMA
2013
---------------------------------------------------------------
Scilab adalah software free dan open source untuk komputasi numerik. Software ini menyediakan lingkungan untuk perhitungan yang dibutuhkan bidangains dan keteknikan. Scilab dirilis sebagai open source dibawahi lisensi CeCILL, dan dapat didownload secara gratis. Scilab tersedia pada sistem operasi GNU/Linux, Mac OS X dan Windows. Scilab juga memiliki dukungan enterprise bagi perusahaan-perusahaan yang membutuhkan dukungan. Scilab menyediakan ratusan fungsi matematis. Software ini memiliki bahasa pemprograman tingkat tinggi dan dapat mengakses struktur data, plot 2D, plot 3D dan fungsi grafis.
Bentuk interface default dari Scilab5.4.0 dibagi menjadi 3 window utama yaitu File Browser, Scilab Console dan Variable Browser. Interface Scilab 5.4.0menggunakan sistem docking, yaitu komponen-komponen interface dapat dipindah pindah sesuai kebutuhan pengguna.
Interpolasi adalah suatu cara untuk mencari nilai di antara beberapa titik data yang telah diketahui. Di dunia nyata, interpolasi dapat digunakan untuk memperkirakan suatu fu ngsi, yang mana fungsi tersebut tidak terdefinisi dengan suatu formula, tetapi didefinisikan hanya dengan data-data atau tabel, misalnya tabel dari hasil percobaan. Ada berbagai macam interpolasi berdasarkan fungsinya, di antaranya adalah interpolasi linier, interpolasi kuadrat, dan interpolasi polinomial. Adapun berbagai metode dalam interpolasi antara lain metode Lagrange dan metode Newton. Kedua metode tersebut menggunakan fungsi polinomial untuk menginterpolasi f (x) pada titik-titik yang diberikan. Bagi para peneliti, interpolasi sering digunakan apalagi bila penelitian yang dilakukan adalah jenis penelitian kuantitatif, artinya banyak data-data yang harus dikumpulkan dan dianalisis.
dpl. : cara menentukan harga fungsi f dititik x* ε [x0,xn] dengan menggunakan informasi dari seluruh atau sebagian titik-titik yang diketahui ( x0, x1, …., xn)
2.2 Jenis – jenis Interpolasi
1. Interpolasi Linear.
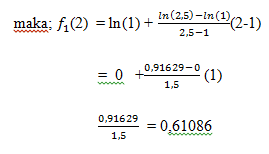
1. Interpolasi Linear.
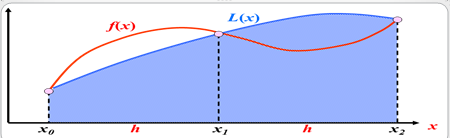
Bentuk interpolasi yang paling sederhana adalah menghubungkan dua titik data dengan garis lurus.teknik ini dinamakan interpolasi linear,dilukiskan secara grafis pada gambar diatas dengan memakai segitiga-segitiga sebangun sehingga diperoleh:
Cara penulisan f1(x) menunjukkan bahwa ini adalah polinom interpolasi orde pertama (interpolasi lanjar).Perhatikan bahwa disamping menyatakan kemiringan garis yang menghubugkan titik-titik, bentuk [f(x1)-f(x0)]/(x1-x0) adalah hampiran (aproksimasi) beda hingga terbagi dari turunan pertama.Umumnya semakin kecil selag diantara titik-titik data, semakin baik hampirannya.
Algoritma Interpolasi
- Tentukan dua titik P1 dan P2 dengan koordinatnya masing-masing (x0,y0) dan (x1,y1)
- Tentukan nilai x dari titik yang akan dicari
- Hitung nilai y dengan
- Tampilkan nilai titik yang baru Q(x,y)
Contoh:
Taksirlah 2 (ln 2) dengan memakai interpolasi linear.yaitu dengan menginterpolasi antara ln 1=0 dan ln 2,5=0,91629
Penyelesaian: Dengan menggunakan persamaan di atas ,interpolasi interpolasi dari x0 =1 sampai x1=2,5
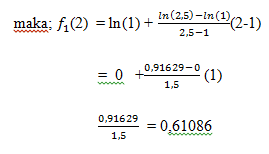
Interpolasi Kuadratik (polinom orde kedua) digunakan untuk mencari titik-titik antara dari 3 buah)
P1 (x0.y0), P2(x1,y1)dan P3(x2,y2) ,polinom kuadrat yang digunakan untuk persamaan ini ialah:
f2(x)=b0+ b1 (x-x0 )+ b2 (x-x0)(x-x1)……………………(P.12.3).
Suatu prosedur yang sederhana dapat dipaki untuk menentukan nilai koefisien-koefisiennya.Untuk b_0
(P.12.3) dengan x=0 dapat dipakai menghitung ;
b0=f(x_0)…………………………………………….(P.12.4)
(P.12.4) dapat disubstitusikan ke (P.12.3) yang dapat dihitung pada x =x_1 untuk
b_1= (f(x1 )-f(x0))/(x2-x0 )………………………………………………(P.12.5)
Akhirnya, (P.12.4) dan (p.12.5) dapat disubstitusikan ke (P.12.3) yang dapat dihitung pada x=x2 dan dipecahakn(setelah melakukan manipulasi aljabar:
P1 (x0.y0), P2(x1,y1)dan P3(x2,y2) ,polinom kuadrat yang digunakan untuk persamaan ini ialah:
f2(x)=b0+ b1 (x-x0 )+ b2 (x-x0)(x-x1)……………………(P.12.3).
Suatu prosedur yang sederhana dapat dipaki untuk menentukan nilai koefisien-koefisiennya.Untuk b_0
(P.12.3) dengan x=0 dapat dipakai menghitung ;
b0=f(x_0)…………………………………………….(P.12.4)
(P.12.4) dapat disubstitusikan ke (P.12.3) yang dapat dihitung pada x =x_1 untuk
b_1= (f(x1 )-f(x0))/(x2-x0 )………………………………………………(P.12.5)
Akhirnya, (P.12.4) dan (p.12.5) dapat disubstitusikan ke (P.12.3) yang dapat dihitung pada x=x2 dan dipecahakn(setelah melakukan manipulasi aljabar:
Contoh:
Cocokkan polinom orde kedua terhadap tiga titik yang dipakai dalam contoh persamaan interpolasi linear:
x0=1 f(x0)=0
x1=4 f(x1)=1,3862944
x2=6 f(x2) =1,7917595
Pakailah polinom tersebut untuk menghitung ln 2
Penyelesaian: Dengan menerapkan persamaan (12.4) maka;
b0 =0
Persamaan (12.5) menghasilkan:b_1=(1,3862944-0)/(4-1) =0,46209813
Dan persamaan (12.6) menghasilkan:
Dengan mensubstitusikan nilai-nilai ini ke (P,12.3) dihasilkan rumus kuadrat
f2(x) =0+0,46209813(x-1)-0,051873116(x-1)(x-4) yang dapat dihitung pada x=2 untuk
f2(x) =0,56584436
Algoritma Interpolasi Kuadratik:
- Tentukan 3 titik input P1(x1,y1), P2(x2,y2) dan P3(x3,y3)
- Tentukan nilai x dari titik yang akan dicari
- Hitung nilai y dari titik yang dicari menggunakan rumus dari interpolasi kuadratik:
- Tampilkan nilai x dan y
3. Interpolasi Kubik
Misal diberikan empat buah titik data ,(x0,y0)(,x1,x1),(x2,y2), dan (x3,y3).Polinom yang mengiterpolasi keempat buah titik itu ialah polinom kubik yang berbentuk :
Polinom 𝑝3𝑥 ditentukan dengan cara berikut:
1.Sulihkan ( xi,yi) kedalam persamaan (p.5.9), i=0,1,2,3. Sehingga diperoleh empat buah persamaan dengan empat buah parameter yang tidak diketahui yaitu
4. Polinom Interpolasi Lagrange
Polinom interpolasi lagrange hanyalah perumusan ulang darri polinom newton yang menghindari komputasi beda-beda terbagi.secara singkat dapat dinyatakan dengan:
Persamaan (12.20) dapat diturunkan secara langsung dari polinom newton (kotak 12.1).Namun, penalaran yang mendasari rumus lagrange dpat langsung ditangkap dengan menyadari bahwa tiap suku Li(x) akan 1 pada x =x_i dan 0 pada titik-titik contoh lainnya. Jadi, tiap hasilkali Li(x)f(x_i) menerima nilai f〖(x〗_i) pada titik contoh x_i.akibatnya ,penjumlahan semua hasilkali yangdinyatakn oleh persamaan (12.20) merupakan polinom orde ke-n unik yang secara eksak melalui seluruh n+1 titik data.
Polinom interplasi lagrange daoat diturunkan kangsung dari rumus newton.ini akan dilakukan untuk kasus orde pertama ,
f1 (x) = f(x0) + (x-x0) f[xx,x0]………………………………(B.12.1.1)
Supaya menurunkan bentuk lagrange ,bedaa-beda terbagi dirumuskan ulang.misalnya. beda terbagi pertama
dapat dirumuskan sebagai :
yang diacu sebagai bentuk simetri,dengan mensubstitusikan persamaan (12.1.2) ke persamaan (B.12.1.1) akan dihasilkan:
Akhirnya dengan mengelompokkan suku-suku yang serupa dan penyederhanaan akan dihasilkan bentuk lagrange :
Contoh program
a. Interpolasi linear
b. Polinom interpolasi lagrange
Output
c. interpolasi kuadrat
Kesimpulan
Scilab adalah software free dan open source untuk komputasi numerik.Software ini menyediakan lingkungan untuk perhitungan yang dibutuhkan bidangains dan keteknikan.
Interpolasi adalah suatu cara untuk mencari nilai di antara beberapa titik data yang telah diketahui. Di dunia nyata, interpolasi dapat digunakan untuk memperkirakan suatu fu ngsi, yang mana fungsi tersebut tidak terdefinisi dengan suatu formula, tetapi didefinisikan hanya dengan data-data atau tabel, misalnya tabel dari hasil percobaan.
Ada berbagai macam interpolasi berdasarkan fungsinya, di antaranya adalah interpolasi linier, interpolasi kuadrat, dan interpolasi polinomial.